기계학습 기말고사를 대비하여 정리한 글
딥러닝 최적화 방법
1. 목적함수 개선
2. 효율적인 학습 전략
3. 규제 기법
4. 하이퍼파리미터 최적화
5. 2차 미분을 이용한 최적화
현대 기계학습의 전략 => 충분히 큰 모델 설계 + 학습 과정에서 여러 규제 기법을 적용한다
규제
규제 기법으로는 가중치 벌칙, 조기 멈츰, 데이터 증강이 있다.
이때 규제는 명시적 규제와 암시적 규제로 나뉜다.
- 명시적 규제 : 목적함수나 신경망 구조를 직접 수정하는 방식 (가중치 감쇠, 드롭아웃)
- 암시적 규제 : 간접적으로 영향을 미치는 방식 ( 조기 멈춤, 데이터 증강)
1. 가중치 벌칙
규제를 적용한 목적함수는 다음과 같다.

규제항 R : 훈련집합과 무관하며 단지 매개변수의 크기에 제약을 가하는 역할만 수행한다.
규제항
매개변수를 작은 값으로 유지한다 즉 모델의 표현력을 제한하는 역할을 한다.
=> 가중치 값을 크지 않게 규제한다.
바이어스는 규제 대상에서 제외된다 (과소 적합 문제로)
1-1. 가중치 감쇠
규제항 R로 L2-norm을 사용하는 규제 기법은 다음과 같다,

그레디언트 식은 다음과 같다.
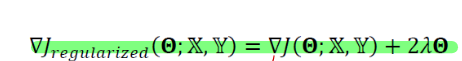
경사하강법 식에 대입하면 다음과 같다.

이때 𝜆 = 0으로 두면 규제 적용이 안된다. 즉 표준 경사하강법이 적용된다
가중치 감쇠는 단지 가중치에 (1-2p 𝜆) 를 곱해준 것과 같다.
이러한 가중치 감쇠를 고려한 업데이트가 반복 적용되면 결국 최종해를 원점 가까이 당기는 효과가 난다.
=> 과적합이 완화되고 일반화 성능이 높아질 수 있다.

1-2. 가중치 감쇠 (선형회귀 적용)
훈련집합 𝕏 = {𝐱1, 𝐱2, ⋯ , 𝐱𝑛} , 𝕐 = {𝑦1, 𝑦2, ⋯ , 𝑦𝑛}을 갖는다고 할 때 다음과 같은 행렬식을 쓸 수 있다.

목적함수는 다음과 같다

이때 가중치 감쇠를 선형회귀에 적용하면 다음과 같은 목적함수가 만들어진다

규제항을 적용한 목적함수로 선형 회귀 문제를 푸는 경우를 리지 회귀라고 한다.
이러한 규제항 목적함수를 미분하면 다음과 같은 식이 만들어진다.

최적의 가중치를 구하는 식은 다음과 같다.
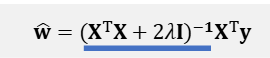
공분산 행렬의 대각요소가 2 𝜆 만틈 증가한다은 것은 패널티를 더해 행렬을 더 크게 만드는 것이다.
이때 더 커진 행렬의 역행렬을 구하면 이 역행렬은 원래보다 작아진다! (역수를 생각하면 된다)
=> 역행렬을 곱하기 때문에 최종적으로 구해지는 최적 가중치의 크기는 작아지게 된다.
리지 회귀에서 가중치를 축소하여 원점으로 당기는 효과가 발생한다
1-3. 가중치 감쇠 (MLP 적용)
규제를 적용한 MLP는 다음과 같아진다

2. 조기 멈춤
학습 시간에 따른 일반화 능력
모델을 학습해봤자 더 좋은 성능을 끌어내기 힘들 것 같다고 판단하면 조기 멈춤을 한다.
모델은 일정시간이 지나면 과잉적합 현상이 발생한다 (훈련 데이터엔 오류가 낮은데 테스트 데이터에서 오류가 발생한다)
따라서 검증 집합의 오류가 최저인 점에서 학습을 멈추는 것이 조기 멈춤 기법이다.
다만 조기 멈춤 기반 학습 알고리즘을 만들 때 지그재그 현상을 고려해야한다. 지그재그 현상에 민감해서 일찍 멈추게 된다면 모델의 학습 능력이 저하된다.

지그재그를 고려하면 다음과 같은 알고리즘을 만들 수 있다

매번 훈련마다 오류를 계산하는 것이 아니라 오류율을 평가하는 주기를 걸어놓고 오류는 체크하는 것이다
p번 성능 향상이 없다면 조기 중단한다.
이때 q 변수는 조사 빈도고 p는 참을성 인자를 의미한다.
3. 데이터 증강
과잉적합을 방지하는 확실한 방법은 큰 훈련집합을 사용하는 것이다. 하지만 데이터 수집은 많은 비용이 드는 작업이다.
따라서 데이터를 인위적으로 변형하여 확대하는 데이터 증강 기법을 사용한다.
- 전통적인 증강: 어파인(선형) 변환(Affine Transformation)을 적용하여 이동, 회전, 크기, 색상, 잡음 등이 반영된 새로운 샘플을 확보합니다 (예: MNIST).
- 한계: 선형 변환만 가능하며, 모든 클래스가 같은 변형을 사용하여 클래스별 특성이 고려되지 못할 수 있다.
- 개선 기법: 모핑(Morphing)을 이용한 형태학적 비선형 변형
- 학습 기반으로 데이터에 맞는 비선형 변환 규칙을 학습하여 어파인 변환에 비해 훨씬 다양한 형태의 확대된 새로운 샘플을 생성한다.

'{Lecture} > Machine Learning' 카테고리의 다른 글
| [기계학습] 딥러닝 최적화 - 효율적인 학습 전략 (1) | 2025.12.14 |
|---|---|
| [기계학습] Multilayer Perceptron : MLP (0) | 2025.10.17 |
| [기계학습] Perceptron (0) | 2025.10.17 |
| [기계학습] 선형대수학 - 행렬 (0) | 2025.10.16 |
| [기계학습] 선형대수학 정리 - 벡터 (0) | 2025.10.16 |




