Perceptron의 구조
입력층과 출력층을 가진다 이때 입력층은 연산을 하지 않으므로 퍼셉트론은 단일층 구조라고 간주한다.
입력층의 i 번째 노드는 특징 벡터의 요소 xi를 담당한다. 이때 항상 입력값으로 1을 받는 것은 바이어스 노드이다. (바이어스 노드를 따로 계산할 때 더하는 것이 아닌 처음부터 입력으로 포함키는 것이다.)
i 번째 입력층 노드와 출력층을 연결하는 선은 가중치 wi를 가진다. 이때 w0는 바이어스이다.

Perceptron의 동작
해당하는 특징값과 가중치를 곱한 결과를 모두 더하여 s 를 구하고 활성함수 T를 적용한다.
이때 활성함수로 계단함수를 사용하므로 최종 출력 y 는 +1 또는 -1 이다.

⭐퍼셉트론으로 OR 논리 게이트 분류 문제 해결이 가능할까?
퍼셉트론으로 OR 논리 게이트는 해결 가능하다.
| AND | 가능 | 선형 구분 가능 |
| OR | 가능 | 선형 구분 가능 |
| NAND | 가능 | 선형 구분 가능 |
| XOR | ❌ 불가능 | 비선형 구분 필요 |
동작을 행렬로 표기하면 행렬 곱은 벡터의 내적 w•x 로 표기가 가능하다.

따라서 퍼셉트론의 동작은 다음과 같이 표현이 가능하다
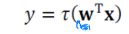
수식상 이점으로는 복잡한 반복 연산을 행렬로 간결하게 표현할 수 있고 구현상 이점으로는 행렬 수식이 병렬 처리가 가능한 연산 단위가 된다는 점이다.
Perceptron의 학습
학습 : 목적 함수
학습으로는 목적함수를 설계해야한다. 퍼셉트론의 매개변수를 w라고 표기하면 매개변수 집합은 θ={w}가 된다.
J(w) 또는 J(θ)라고 표기한다.
목적 함수의 조건은 다음과 같다
1. J(w) >=0 이다.
2. w 가 최적, 즉 모든 샘플을 맞히면 J(w) = 0 이다.
3. 틀리는 샘플이 많은 w 일수록 J(w)는 큰 값을 갖는다.

- → 입력 샘플 xk에 대한 모델의 선형 예측값
- → 실제 정답 레이블 (보통 -1 또는 +1)
- 두 값의 부호가 다르면 오분류!
(즉, 잘못 분류된 데이터일수록 − −yk(wTxk) 값이 커짐)
경사 하강법
경사 하강법은 현대 기계학습의 핵심이다.
비용 함수를 최소화하기 위해 현재 위치에서 비용함수의 기울기 계산을 진행한 다음 기울기의 반대 방향(하강)으로 이동시키는것을 말한다.

경사 하강법 : 기울기 Gradient 계산
퍼셉트론이나 신경망에서 가중치를 업데이트할 때의 기본 원리는 기울기 계산이다.
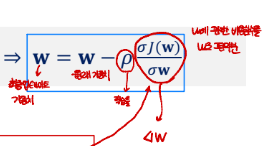
손실 함수의 기울기(gradient)는 W를 얼마나, 어떤 방향으로 바꿔야 손실이 줄어드는지를 알려준다.
ρ 는 학습률(learning rate)이며 한 번에 이동하는 크기 (너무 크면 발산, 너무 작으면 수렴이 느림)
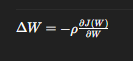
경사(gradient)의 반대 방향으로 조금 이동하면서 가중치를 업데이트 하는것이 학습이다.


| Wi | i번째 가중치 | 학습 중인 파라미터 |
| ρ | 학습률 (learning rate) | 한 번에 가중치를 얼마나 바꿀지 조절 |
| xki | k번째 샘플의 i번째 입력값 | 즉, 입력 벡터의 구성요소 |
| yk | k번째 샘플의 실제 정답(label) | +1 또는 -1 |
| Y | 오분류된 샘플 집합 | 잘못 분류된 데이터만 포함 |
Perceptron 알고리즘
델타 규칙식을 이용해서 학습 알고리즘을 구성한다.
알고리즘 3-1: 배치 버전 (Batch Perceptron)
- 한 epoch(전체 데이터 1회 학습) 동안 모든 샘플을 확인
- 오분류된 샘플을 전부 모아서 한꺼번에 가중치 수정
즉, 한 번의 업데이트에 여러 샘플의 영향이 누적된다.

1. 가중치 w 초기화
2. 모든 샘플을 한 바퀴 돌며 오분류된 것만 집합 Y'에 추가
3. Y'이 비어 있지 않으면 (즉, 오분류 존재 시)
w_i = w_i + ρ Σ(y_k * x_ki) ← 델타 규칙 적용
4. 모든 샘플이 올바르게 분류될 때까지 반복
특징
- 안정적 (한 번에 많은 샘플 평균 반영)
- 하지만 느림 (매 epoch마다 전체 데이터 확인)
- 수렴 속도는 느려도 안정적임
알고리즘 3-2: 확률적(=온라인) 버전 (Stochastic Perceptron)
작동 원리
- 샘플을 하나씩 확인하면서 바로 업데이트
- 오분류된 순간 바로 가중치 조정 수행
즉, 데이터가 들어올 때마다 즉각 학습하는 방식이다.

1. w 초기화
2. 샘플 순서 섞기
3. 각 샘플(x_k, y_k)에 대해:
- 예측 y = f(wᵗx)
- 오분류 시: w_i = w_i + ρ * y_k * x_ki
4. 한 epoch 동안 오분류가 없으면 종료
특징
- 빠름 (즉시 업데이트)
- 약간의 불안정성 (순서에 따라 결과 달라질 수 있음)
- 실시간 학습(online learning)에 적합
'{Lecture} > Machine Learning' 카테고리의 다른 글
| [기계학습] 딥러닝 최적화 - 규제 ( 가중치 감쇠, 조기 멈춤, 데이터 증강) (0) | 2025.12.14 |
|---|---|
| [기계학습] 딥러닝 최적화 - 효율적인 학습 전략 (0) | 2025.12.14 |
| [기계학습] Multilayer Perceptron : MLP (0) | 2025.10.17 |
| [기계학습] 선형대수학 - 행렬 (0) | 2025.10.16 |
| [기계학습] 선형대수학 정리 - 벡터 (0) | 2025.10.16 |




