Matrix — 선형대수학과 기계학습의 핵심
행렬(Matrix)의 개념
여러 벡터를 모은 2차원 숫자 배열을 말한다. 훈련집합의 특징들을 행 또는 열로 표현한 것도 행렬이라고 할 수 있다.
행렬은 다항식을 간결하게 표현할 수 있고 벡터화를 통한 고속 연산 구현이 가능하다.

예를 들어, Iris 데이터셋에서 150개의 샘플과 4개의 특징(feature)을 가진다면
전체 데이터는 X∈R ^150×4 로 표현된다.
행렬 A의 전치행렬

행과 열을 바꾼 행렬을 전치 행렬이라고 한다.
특수한 행렬들

- 정사각행렬: 행과 열의 수가 같은 행렬
- 대각행렬: 주 대각선을 제외한 모든 항들이 0
- 단위행렬: 대각행렬이면서, 대각선의 항들이 모두 1
- 대칭행렬: n x n 행렬이 A = A^T이다.
행렬 연산 기초
행렬은 덧셈, 스칼라 곱, 그리고 행렬 곱으로 조합될 수 있으며 기계학습에서는 “입력 데이터 × 가중치 행렬 = 예측값” 형태로 사용된다. 즉, 선형모델의 핵심 연산은 결국 행렬 연산이다.
1. 행렬의 덧셈
두 행렬 A와 B의 크기가 같을 때만 가능하다. 각 요소 위치가 같은 항끼리 더하여 새로운 행렬 C를 얻는다

2. 스칼라 곱셈
스칼라(하나의 실수) 를 행렬의 모든 요소에 곱한다. 이 연산은 크기를 조절하되 방향(구조)은 변하지 않는다.

3. 행렬 곱셈
앞의 행렬 A의 열 개수와 뒤의 행렬 B의 행 개수가 같아야 한다. 결과 행렬 C의 크기는 A의 행 × B의 열이 된다.

- 교환법칙은 성립하지 않음: AB≠BA
- 분배법칙 및 결합법칙은 성립: A(B+C)=AB+AC, (AB)C=A(BC)
선형 종속 (Linear Dependence)
선형 종속이란, 하나의 벡터가 나머지 벡터들의 선형 결합으로 표현될 수 있을 때를 말한다.

여기서 적어도 하나 이상의 ci 가 0이 아니라면, 이 벡터들은 선형 종속이다. 즉, 벡터들 사이에 중복된 정보가 있다는 뜻이다.
데이터 관점에서 보면, 어떤 특징이 다른 특징의 선형결합으로 표현될 수 있다면 그 특징은 새로운 정보를 제공하지 않는다.
이런 상황은 다중공선성(multicollinearity)이라 하며, 회귀모델 학습 시 가중치가 불안정하게 변하는 원인이 된다.
선형 독립 (Linear Independence)

이 식을 만족하는 해가 오직 일 때, 그 벡터 집합은 선형 독립(linearly independent) 이라고 한다.
선형 독립한 벡터들은 서로 중복되지 않은 방향을 가지며, 데이터 표현의 다양성과 정보량을 극대화한다.
역행렬 (Inverse Matrix)
정사각행렬 A에 대해, 다음 조건을 만족하는 행렬 A^-1 이 존재할 때 우리는 그것을 A의 역행렬이라 부른다

여기서 I는 단위행렬(Identity matrix)이다. 즉, 역행렬은 행렬의 “역연산”으로, 입력에 어떤 변환을 가한 후 다시 원래 상태로 되돌릴 수 있게 해준다.
역행렬 존재 판별식
행렬의 역행렬이 존재하려면, 다음 조건을 만족해야한다.
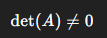
즉, 행렬식(Determinant)이 0이 아니어야 한다. 이는 행렬이 선형 독립된 열 벡터를 가진다는 의미와 동일하다.
역행렬 구하기

가장 단순한 2×2 행렬의 역행렬은 다음과 같이 계산된다. 여기서 ad−bc가 0이라면 역행렬은 존재하지 않는다.
이때 A의 두 열 또는 두 행이 서로 선형 종속임을 의미한다
고유값(Eigenvalue)과 고유벡터(Eigenvector)

행렬 A에 대해, 다음 조건을 만족하는 스칼라 λ와 벡터 v가 존재하면
λ를 고유값, 를 고유벡터라고 한다.
이 관계를 만족하는 λ 는 다음 방정식으로 구한다.
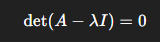
고유값과 고유벡터는 머신러닝에서 매우 중요한 의미를 갖는다.
예를 들어 PCA(주성분 분석)에서는 공분산행렬의 고유벡터가 데이터의 최대 분산 방향(주성분)을 의미하며, 고유값은 그 방향의 중요도(분산의 크기)를 나타낸다.
즉, 가장 큰 고유값에 대응하는 고유벡터가 데이터의 가장 중요한 축이 된다.
행렬 분해 (Matrix Decomposition)
행렬 분해는 복잡한 행렬을 더 단순한 구성요소로 나누는 과정이다. 이는 계산 효율성을 높이고, 데이터의 구조적 의미를 파악하는 데 사용된다.
고유값 분해
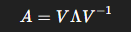
대각행렬 λ 에 고유값이, V에 고유벡터가 들어간다. 대칭행렬의 경우 항상 실수 고유값을 가지며, PCA나 스펙트럼 분석에 활용된다.
'{Lecture} > Machine Learning' 카테고리의 다른 글
| [기계학습] 딥러닝 최적화 - 규제 ( 가중치 감쇠, 조기 멈춤, 데이터 증강) (0) | 2025.12.14 |
|---|---|
| [기계학습] 딥러닝 최적화 - 효율적인 학습 전략 (1) | 2025.12.14 |
| [기계학습] Multilayer Perceptron : MLP (0) | 2025.10.17 |
| [기계학습] Perceptron (0) | 2025.10.17 |
| [기계학습] 선형대수학 정리 - 벡터 (0) | 2025.10.16 |




