컴파일러 기말고사를 대비하여 정리한 글입니다.
1. Pushdown Automata(PDA)를 설명하기
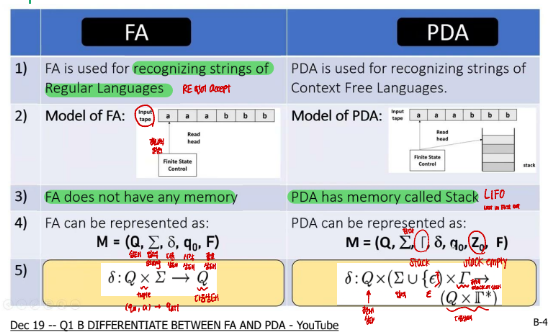
Pushdown Automata(PDA)는 문맥자유언어(Context-Free Language, CFL)를 인식하기 위한 계산 모델이다.
이는 유한 오토마타(Finite Automata, FA)에 스택(Stack)이라는 추가적인 기억 장치를 결합한 형태이다.
유한 오토마타는 상태만을 이용해 입력을 처리하므로, 입력의 개수를 기억하거나 중첩 구조를 처리할 수 없다. 반면 PDA는 스택을 사용하여 이전 입력에 대한 정보를 저장할 수 있으므로, 괄호의 짝 맞추기나 aⁿbⁿ과 같은 언어를 인식할 수 있다.
형식적으로 PDA는 다음과 같은 7-튜플로 정의된다.
- Q: 상태의 유한 집합
- Σ: 입력 알파벳
- Γ: 스택 알파벳
- δ: 전이 함수
- q₀: 시작 상태
- Z₀: 초기 스택 기호
- F: 종료 상태 집합
전이 함수 δ는 현재 상태, 현재 입력 기호(또는 ε), 스택의 top을 동시에 고려하여 다음 상태와 스택의 변화를 결정한다. 이 점이 FA와 PDA의 가장 큰 차이점이다.

2. PDA에서 Stack Marker를 사용하는 식별 과정 보이기
Stack marker는 스택의 바닥을 표시하기 위한 특수 기호로, 보통 Z₀ 또는 $로 표현된다. 이는 PDA가 스택이 완전히 비워졌는지를 정확히 판단하기 위해 사용된다.
예를 들어 언어 L = { aⁿbⁿ | n ≥ 1 }을 인식하는 PDA를 생각해보자.
식별 과정은 다음과 같다.
- PDA는 시작 시 스택에 stack marker Z₀를 push한다.
- 입력에서 a를 읽을 때마다 스택에 기호 A를 push한다.
- 입력에서 b를 읽을 때마다 스택에서 A를 pop한다.
- 입력이 모두 소진되었을 때, 스택의 top이 Z₀라면 문자열을 accept한다.
이때 stack marker가 없다면, 스택이 비었는지 여부를 명확하게 판단할 수 없으므로 정상 종료 여부를 확인할 수 없다. 따라서 stack marker는 PDA의 종료 조건을 명확히 하는 핵심 요소이다.


3. 문법의 모호성(ambiguity)과 재귀순환 문제, 그리고 개선책
3-1. 문법의 모호성(Ambiguity)
문법의 모호성이란 하나의 문자열에 대해 두 개 이상의 서로 다른 파싱 트리(parse tree)가 존재하는 경우를 의미한다.
E → E + E | E * E | id
문자열 id + id * id는 다음 두 가지 방식으로 해석될 수 있다.
- (id + id) * id
- id + (id * id)
이처럼 동일한 문자열에 대해 서로 다른 파싱 트리가 만들어질 수 있으면, 해당 문법은 모호한 문법이다. 모호한 문법은 컴파일러에서 연산 순서를 결정할 수 없기 때문에 바람직하지 않다.
개선책
- 연산자 우선순위와 결합법칙을 명확히 반영한 비모호 문법으로 재작성한다.
3-2. 재귀순환 문제(Left Recursion)
재귀순환 문제, 특히 좌재귀(left recursion)란 다음과 같은 형태의 문법을 말한다.
E → E + T | T
LL 파싱과 같은 top-down 파싱에서는 이 문법을 사용할 경우 무한 재귀에 빠지게 된다.
개선책: 좌재귀 제거
좌재귀는 다음과 같이 제거할 수 있다.
E → T E'
E' → + T E' | ε
이렇게 변환하면 LL 파서에서도 정상적으로 파싱이 가능해진다
4. LR 파싱 테이블을 주고 간단한 수식을 파싱하기
LR 파싱은 bottom-up 방식의 파싱 기법으로, 입력 문자열을 점점 줄여가며 시작 기호로 만드는 방식이다.
LR 파서는 ACTION 테이블과 GOTO 테이블을 사용한다.
- ACTION 테이블: shift, reduce, accept 중 어떤 동작을 할지 결정
- GOTO 테이블: reduce 이후 비단말 기호에 대해 이동할 상태를 결정
파싱 과정은 다음을 반복한다.
- 현재 상태와 다음 입력 기호를 보고 ACTION 테이블을 참조한다.
- shift라면 입력 기호와 상태를 스택에 push한다.
- reduce라면 규칙의 RHS 길이만큼 스택을 pop하고, LHS 비단말과 GOTO를 통해 새로운 상태를 push한다.
- accept가 나오면 파싱이 종료된다.

| 구분 | SHIFT | REDUCE |
| 입력 소비 | O | X |
| 스택 변화 | 증가 | 감소 후 증가 |
| 기준 | ACTION 테이블 | ACTION + GOTO |
| 의미 | 아직 판단 안 함 | 규칙 확정 |
5. LL 파싱 테이블을 주고 간단한 수식을 파싱하기
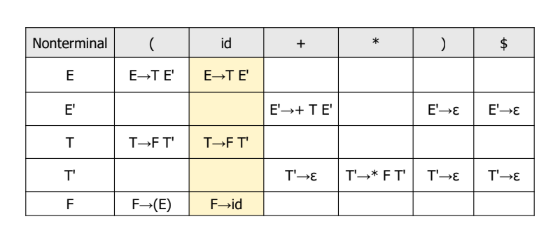
LL 파싱은 top-down 방식으로, 시작 기호에서 출발하여 입력 문자열을 생성해 나가는 방식이다. LL 파싱은 LL 파싱 테이블 하나만을 사용한다.
파싱 과정은 다음과 같다.
- 스택의 top이 비단말이면, 현재 입력 기호와 LL 테이블을 참조하여 적용할 규칙을 선택한다.
- 선택된 규칙의 RHS를 스택에 push한다.
- 스택의 top이 단말이고 입력 기호와 같으면, 둘 다 제거한다.
- 입력과 스택이 동시에 종료되면 파싱 성공이다.
LL 파싱은 좌재귀가 없고 FIRST/FOLLOW 충돌이 없는 문법에서만 가능하다.

6. FIRST 집합을 구하는 이유와 FIRST 집합 구하기
FIRST 집합을 구하는 이유
FIRST 집합은 LL 파싱에서 어떤 생산 규칙을 선택할지 결정하기 위해 사용된다.
즉, 특정 비단말이 확장될 때 첫 번째로 등장할 수 있는 단말 기호의 집합이다.
LL 파싱 테이블에서
FIRST 집합 계산 규칙
- 단말 기호 a에 대해
FIRST(a) = {a} - ε 생산이 있으면
ε ∈ FIRST(A) - A → X₁X₂...Xₙ일 때
- FIRST(X₁)에 ε가 없으면 그것으로 종료
- ε가 있으면 X₂, X₃를 순서대로 검사
7. FOLLOW 집합을 사용하는 이유와 집합 구하기
FOLLOW 집합을 사용하는 이유
FOLLOW 집합은 ε-생산을 선택해야 할 경우를 결정하기 위해 사용된다.
즉, 어떤 비단말 뒤에 올 수 있는 단말 기호들의 집합이다.
LL 파싱 테이블에서 A → ε 규칙은
FOLLOW 집합 계산 규칙
- 시작 기호 S에 대해
$ ∈ FOLLOW(S) - A → αBβ이면
FIRST(β) - {ε} ⊆ FOLLOW(B) - A → αB 이거나 FIRST(β)에 ε가 포함되면
FOLLOW(A) ⊆ FOLLOW(B)
'{Lecture} > Compiler' 카테고리의 다른 글
| [컴파일러] BNF 정리 (0) | 2025.10.23 |
|---|---|
| [컴파일러] 촘스키 언어 계층 정리 - 문법 정리 (0) | 2025.10.23 |
| [컴파일러] 컴파일러의 구조 (Front-End와 Back-End 구성과 역할) (0) | 2025.10.23 |
| [컴파일러] NFA -> DFA 변환 (0) | 2025.10.23 |
| [컴파일러] 컴파일러란? (0) | 2025.10.22 |




