728x90
Deterministic Finite Automata (DFA)
- 어떤 상황에서도 이동(transition)을 선택할 여지가 없다.
→ 즉, 현재 상태와 입력 기호가 주어지면 다음 상태가 단 하나로 결정된다.
→ “결정적(Deterministic)”이라는 말은 바로 이 뜻이다.
Non-deterministic Finite Automata (NFA)
- 적어도 한 경우에서 다음 상태로 가는 선택지가 여러 개일 수 있다.
→ 즉, 같은 상태에서 같은 입력 기호로 여러 개의 전이(transition) 가 가능하거나,
→ ε(엡실론) 전이처럼 입력 없이 이동하는 경우가 있을 수 있다. - 입력 문자열을 받아들인다는 것(accept) 은
→ 여러 가능한 경로 중 하나라도 최종 상태(final state)에 도달할 수 있다면 Accept (수용)
→ 모든 경로가 최종 상태에 도달하지 못하면 Reject (거부)
DFA: 입력에 따라 이동 경로가 딱 하나로 정해지는 기계
NFA: 입력 하나에 대해 여러 이동 경로 중 하나라도 성공하면 통과되는 기계
NFA -> DFA 변환
NFA에서 DFA로 변환할 때 ε-closure(ε-닫힘)는 어떤 상태에서 ε-transition(ε-이동)을 통해 도달할 수 있는 모든 상태 집합을 의미한다.
즉, 특정 상태 q에서 입력 없이(ε) 이동할 수 있는 모든상태들을 포함하는 집합을 말한다.
| ε-closure(s) | NFA의 한 상태 s로부터 ε(엡실론) 전이만을 따라 도달할 수 있는 모든 상태들의 집합. |
| ε-closure(T) | 집합 T 안에 있는 어떤 NFA 상태 s로부터 ε 전이만을 따라 도달할 수 있는 모든 상태들의 집합.즉, T에 속한 모든 s에 대한 ε-closure(s) 의 합집합으로 표현된다. |
| move(T, a) | 집합 T에 속한 어떤 상태로부터 입력 기호 a를 통해 전이할 수 있는 모든 NFA 상태들의 집합. |
NFA -> DFA 변환 알고리즘
# NFA → DFA 변환 알고리즘 (Subset Construction)
Input:
NFA = (Q, Σ, δ, q0, F)
Q = NFA 상태 집합
Σ = 입력 기호 집합
δ = 전이 함수
q0 = 시작 상태
F = 종료 상태 집합
Output:
DFA = (Dstates, Σ, Dtran, q0', F')
------------------------------------------------------
# 1. 초기화
q0' = ε-closure(q0) # NFA 시작 상태의 ε-closure 계산
Dstates = { q0' } # DFA의 상태 집합
mark(q0') = unmarked # 아직 방문 안 함
# 2. 반복 시작
while ( there exists an unmarked state T in Dstates ):
mark(T) as visited # T를 방문 처리
for each input symbol a in Σ:
U = ε-closure(move(T, a)) # T에서 a 입력 후 ε로 도달 가능한 상태들
if (U not in Dstates): # 새로운 상태라면
add U to Dstates # Dstates에 추가
mark(U) = unmarked # 방문 전 상태로 표시
Dtran[T, a] = U # DFA 전이표에 등록
# 3. 종료 상태 결정
F' = { S in Dstates | S ∩ F ≠ ∅ } # NFA의 종료 상태를 포함하는 집합이면 DFA 종료 상태
------------------------------------------------------
Output: Dstates, Dtran, q0', F'
move(T, a)
- 집합 T 안의 상태들 중, 입력 a 를 읽고 갈 수 있는 모든 상태들의 집합을 구한다.
→ “입력 a 를 한 번 소비했을 때 도달 가능한 상태들”
ε-closure(...)
- 위에서 도착한 상태들로부터 ε 전이만 따라가며 갈 수 있는 모든 상태들을 추가로 포함한다.
→ “ε-전이로 더 확장된 상태 집합”
⭐ ε-closure(move(T, a))
= “입력 a를 처리한 뒤, ε로 더 갈 수 있는 모든 상태들의 집합”
이해하는데 도움이 됐던 예시
T = {q0}
q0 --a--> q1
q1 --ε--> q2
move(T, a) = {q1}
ε-closure(move(T, a)) = {q1, q2}
- a를 입력으로 이동하면 q1에 도착하고, 그 다음 ε-전이로 q2까지 갈 수 있으니, 둘 다 포함된 집합이 된다.
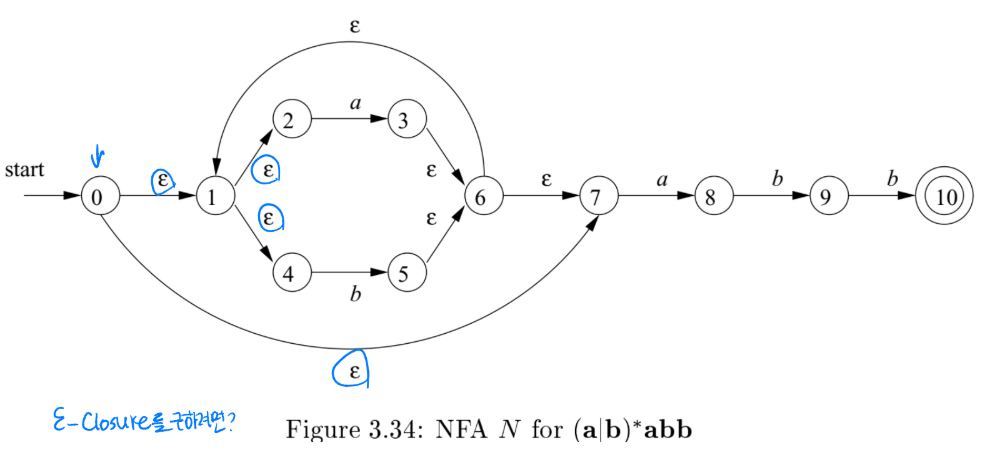
다음과 같이 표로 정리할 수 있습니다.
| 현재 DFA 상태 (NFA 집합) | 입력 | move(T, a) | ε-closure(move(T, a)) 결과 |
다음 DFA 상태
|
| A = {0,1,2,4,7} | a | {3,8} | {1,2,3,4,6,7,8} | B |
| b | {5} | {1,2,4,5,6,7} | C | |
| B = {1,2,3,4,6,7,8} | a | {3,8} | {1,2,3,4,6,7,8} | B (자기 자신) |
| b | {5,9} | {1,2,4,5,6,7,9} | D | |
| C = {1,2,4,5,6,7} | a | {3,8} | {1,2,3,4,6,7,8} | B |
| b | {5} | {1,2,4,5,6,7} | C (자기 자신) | |
| D = {1,2,4,5,6,7,9} | a | {3,8} | {1,2,3,4,6,7,8} | B |
| b | {5,10} | {1,2,4,5,6,7,10} | E | |
| E = {1,2,4,5,6,7,10} | a | {3,8} | {1,2,3,4,6,7,8} | B |
| b | {5} | {1,2,4,5,6,7} | C |


728x90
'{Lecture} > Compiler' 카테고리의 다른 글
| [컴파일러] 촘스키 언어 계층 정리 - 문법 정리 (0) | 2025.10.23 |
|---|---|
| [컴파일러] 컴파일러의 구조 (Front-End와 Back-End 구성과 역할) (0) | 2025.10.23 |
| [컴파일러] 컴파일러란? (0) | 2025.10.22 |
| [컴파일러] 3주차 Grammar Basic (0) | 2025.09.16 |
| [컴파일러] Programming Language Basics (0) | 2025.09.11 |



