✏️해당 포스트는 인프런 알고리즘 코딩테스트 핵심이론 강의를 토대로 정리한 내용입니다.
⭐너비 우선 탐색 (BFS) 이란?
너비 우선 탐색도 그래프를 완전 탐색하는 방법 중 하나로 시작 노드에서 출발해 시작 노드를 기준으로 가까운 노드를 먼저 방문하면서 탐색하는 알고리즘이다. 그래프 완전 탐색이라는 점은 DFS와 같다.
특징은 FIFO 탐색(선입선출 방식)을 하며 Queue 자료구조를 이용한다.
⭐DFS와의 차이
- DFS (깊이 우선 탐색)
- 한 경로를 끝까지 파고들었다가 더 이상 못 가면 되돌아와서 다른 경로를 탐색
- 즉, 깊게 → 깊게 → 끝까지 간 다음 백트래킹
- 주로 스택(Stack) 구조(또는 재귀 호출)로 구현
- 미로에서 한 길을 끝까지 들어갔다가 막히면 뒤로 돌아와 다른 길 시도하는 방식
- BFS (너비 우선 탐색)
- 시작 정점에서 가까운 노드(거리 1)를 먼저 모두 방문하고, 그 다음 거리 2, 3 … 순서대로 차례대로 탐색
- 즉, 레벨 순서대로 탐색
- 주로 큐(Queue) 구조로 구현
- 미로에서 출발점에서 가까운 칸부터 동심원 모양으로 탐색해 나가는 방식
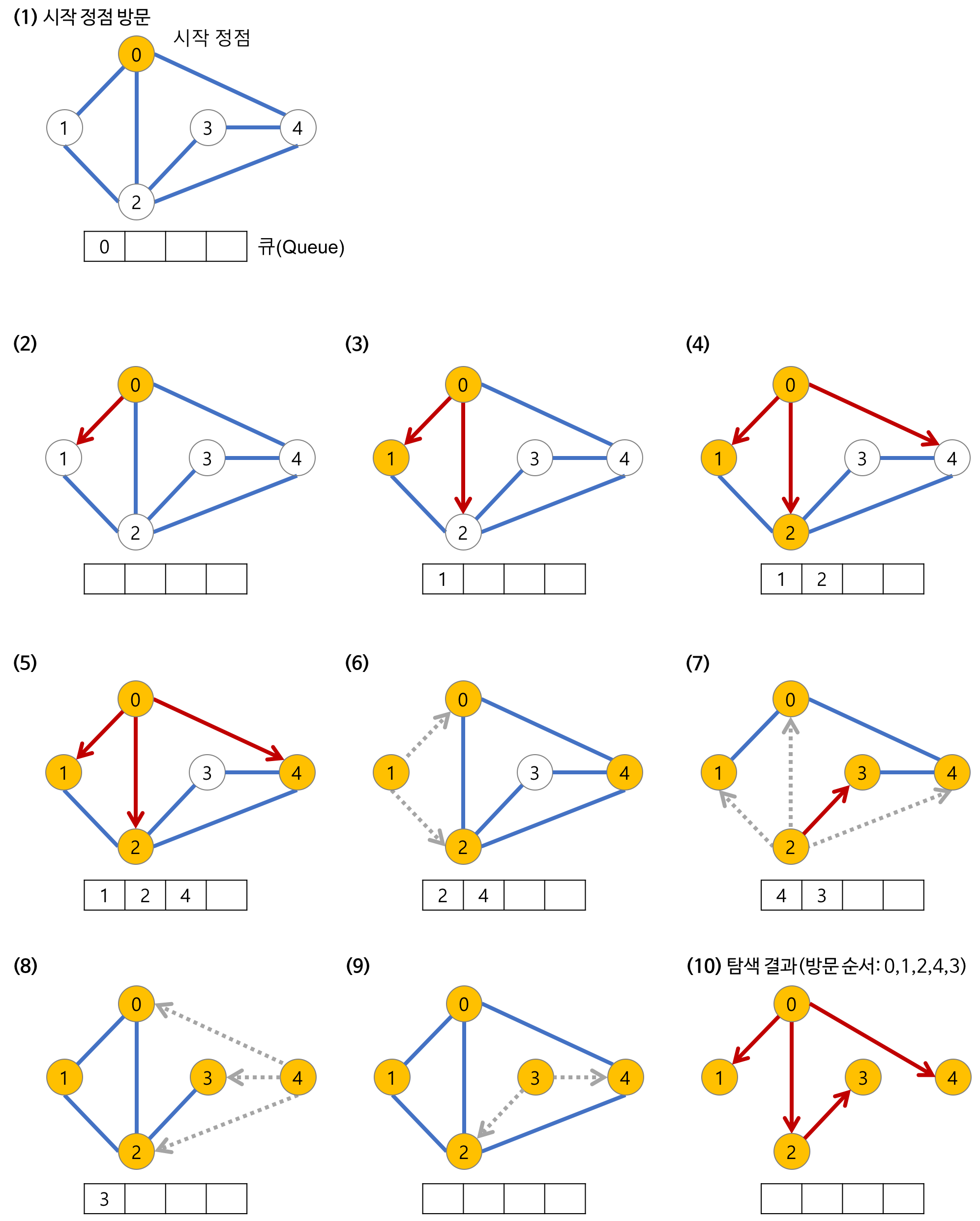
그림 출처 : https://gmlwjd9405.github.io/2018/08/15/algorithm-bfs.html
[알고리즘] 너비 우선 탐색(BFS)이란 - Heee's Development Blog
Step by step goes a long way.
gmlwjd9405.github.io
⭐너비 우선 탐색 (BFS) 핵심 이론
1. BFS를 시작할 노드를 정한 후 사용할 자료구조 초기화하기
BFS도 DFS와 마찬가지로 방문했던 노드는 다시 방문하지 않는다. 따라서 방문 노드를 체크할 배열이 필요하다. 그래프를 인접 리스트로 표현한다. 이때 탐색을 할 땐 큐를 사용한다.

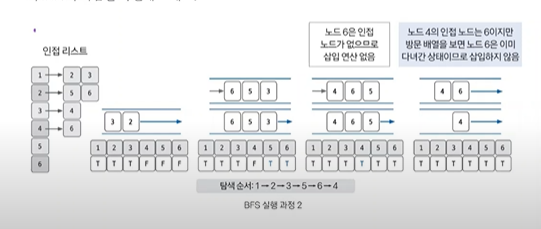
2. 큐에서 노드를 꺼낸 후 꺼낸 노드의 인접 노드를 다시 큐에 삽입한다.
큐에서 노드를 꺼내면서 인접노드를 큐에 삽입한다. 이때 방문 배열을 체크하여 이미 방문한 노드는 큐에 삽입하지 않는다. 또한 큐에서 꺼낸 노드는 탐색 순서에 기록한다

위 그림의 경우 1을 꺼내면서 탐색 순서 1을 기록하고 인접노드 2,3을 순서대로 큐에 삽입했다.
3. 큐 자료구조에 값이 없을 때까지 반복하기
큐에 노드가 없을 때까지 앞선 과정을 반복한다. 선입선출 방식으로 탐색하므로 탐색 순서가 DFS와 다름을 확인할 수 있다.
이미 방문한 노드는 큐 삽입을 하지 않는다.
간단한 예제 코드 BFS
import java.util.*;
public class Main {
static boolean[] visited;
static List<List<Integer>> graph = new ArrayList<>();
public static void main(String[] args) {
int n = 5; // 노드 개수 (1~5)
// 그래프 초기화
for (int i = 0; i <= n; i++) {
graph.add(new ArrayList<>());
}
// 간선 추가 (양방향)
addEdge(1, 2);
addEdge(1, 3);
addEdge(2, 4);
addEdge(3, 5);
visited = new boolean[n + 1];
System.out.println("DFS 탐색 순서:");
dfs(1); // 1번 노드부터 탐색 시작
}
static void addEdge(int u, int v) {
graph.get(u).add(v);
graph.get(v).add(u);
}
static void dfs(int node) {
visited[node] = true;
System.out.print(node + " ");
for (int next : graph.get(node)) {
if (!visited[next]) {
dfs(next);
}
}
}
}
- visited[] 배열로 방문 여부 체크
- dfs(node) → 현재 노드를 방문 처리
'{Algortihm}' 카테고리의 다른 글
| [JAVA] 자바 코딩 테스트 문법 정리 (0) | 2025.09.25 |
|---|---|
| [알고리즘] 문자 및 숫자 알파벳 변환 정리 (0) | 2025.09.25 |
| [알고리즘] 백트래킹 (Backtracking) (0) | 2025.09.11 |
| [알고리즘] DFS 깊이 우선 탐색 (3) | 2025.07.30 |



